Bài toán phát biểu như sau: Hãy vẽ một biểu đồ từ tập hợp lớn các điểm nằm rải rác khác nhau trên cùng một mặt phẳng, mọi điểm đều được kết nối bởi các đường thẳng giữa chúng.
Nếu mỗi điểm (hay đỉnh) được tô màu, thì sẽ cần tối thiểu bao nhiêu màu sắc khác nhau sao cho hai điểm liên kết với nhau có cùng màu?
Không dễ để giải bài toán này, khi về mặt lý thuyết, nó có khả năng ẩn chứa một con số vô tận các đỉnh được kết nối. Kể từ khi được nhà toán học Edward Nelson tại Đại học Princeton trình bày vào năm 1950, chưa có ai giải quyết nó một cách triệt để.
Trong suốt nhiều năm, những nỗ lực của giới toán học đã chỉ ra rằng: sẽ phải cần tối thiểu 4 màu, nhưng cũng không vượt quá 7 màu.
Grey, vốn là chuyên gia nghiên cứu trong lĩnh vực lão khoa - nhằm kéo dài tuổi thọ của con người - vừa công bố một bài báo trên arXiv để thu gọn lại đáp án của bài toán.
Trước đây, giới toán học tin rằng đó có thể là 4,5,6 hoặc 7, tuy nhiên trong lời giải của mình, Grey đã chỉ ra không thể là 4 (ngay cả máy tính cũng không thể vẽ được bằng 4 màu), mà chỉ có thể là 5,6 hoặc 7.
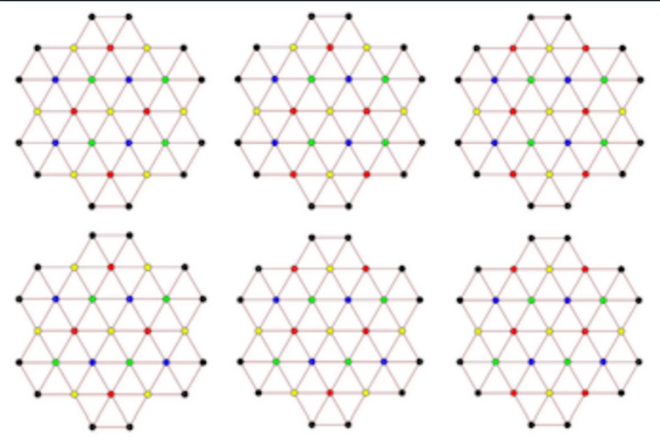
Không thể vẽ được biểu đồ với 3 màu, nhưng con số 4 đã gây nhiều tranh cãi cho tới khi Grey công bố lời giải của mình. Ảnh: Live Science
Biểu đồ của Grey bao gồm 1581 đỉnh (điểm), được sắp xếp theo cách mà chúng ta không thể vẽ nó chỉ với 4 màu mà phải cần ít nhất 5 màu khác nhau.

Biểu đồ của Grey. Ảnh: Live Science
Tuy nhiên, điều đó không có nghĩa con số 5 chính là giá trị tuyệt đối nhỏ nhất. Từ lâu, giới toán học đã biết rằng có thể vẽ một biểu đồ như vậy bằng 6 hay 7 màu. Chẳng hạn, lời giải do John Isbell đưa ra vào năm 1950 cần dùng đến 7 màu.
Con số tối thiểu cho đến nay vẫn còn là một bí ẩn. Tuy nhiên, nhờ Grey mà chúng ta biết rằng cần nhiều hơn 4.
Nguồn: Live Science