Thiên tài toán học khác người đó chính là Grigori Perelman, một trong những bộ óc vĩ đại nhất của thế kỷ 21.
Hơn một thập kỷ trước đây, Perelman đã chào tạm biệt sự nghiệp và đời sống trước công chúng. Khi đó, ông đã nổi tiếng thế giới nhờ giải được một trong những bài toán khó nhất của thiên niên kỷ có từ thế kỷ 18. Nguồn gốc bài toán này là Königsberg, một thành phố cổ của vương quốc Phổ và Đức cho tới năm 1945, ngày nay là thành phố Kaliningrad thuộc Nga.
Königsberg có 7 chiếc cầu trên sông Pregel nối hai bờ thành phố và hai cù lao trên sông. Từ xưa, người dân nơi đây đã đặt ra câu hỏi mà sau này trở thành bài toán nổi tiếng:
Liệu có thể rời nhà từ một trong bốn vùng của Königsberg, băng qua cả 7 cây cầu một lần và trở về điểm xuất phát ban đầu?
Lời giải cho bài toán này không chỉ khó khăn hơn chúng ta tưởng mà còn dẫn tới sự ra đời của những bộ môn toán học mới, trong đó có topo học hay hình học topo (topology).
Cuối cùng, nhà toán học vĩ đại Leonhard Euler đã đưa ra câu trả lời vào năm 1735: không thể thực hiện được. Điều gây tò mò nhất là một bước nhảy vọt về khái niệm trong khi giải quyết bài toán này. Euler nhận ra rằng khoảng cách giữa các cây cầu không liên quan gì. Điều thật sự có ý nghĩa là cách mà các tòa nhà được kết nối với nhau, có nghĩa là lý thuyết không chỉ giới hạn ở thành phố Konigsberg mà được áp dụng cho tất cả những cấu hình đồng dạng về mặt topo học.
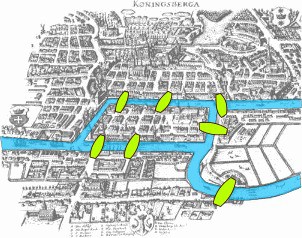
(Ảnh: Wikipedia)
Đó là sự khởi đầu của các khái niệm topo học mà ngày nay là nền tảng cho tất cả các bản đồ tàu điện ngầm của thế giới, để chỉ rõ cho người đi tàu những gì họ cần biết: làm cách nào để tới được nơi họ muốn đến.
Mặc dù nguồn gốc của topo học liên quan tới những cây cầu ở Königsberg, mãi tới cuối thế kỷ 19, topo học mới nằm trong tay của nhà toán học được tôn kính và nổi tiếng nhất, Henri Poincaré của nước Pháp, người đã làm cho topo học trở thành một phương pháp xem xét các hình dạng hoàn toàn mới và mạnh mẽ.
Topo học
Theo UOL News, ý tưởng chính của topo học là khi bạn nghiên cứu một vật thể, điều quan trọng nhất là các đặc điểm của nó chứ không phải bản thân vật thể. Nếu hai vật thể cùng chia sẻ các đặc điểm chung, chúng phải được nghiên cứu vì các kết quả đó có thể được mở rộng cho tất cả mọi vật thể cùng chia sẻ các đặc điểm chung, hay còn gọi là vật thể đồng phôi (homeoform).
Topo học chuyên nghiên cứu về sự bảo tồn của các bề mặt, khi các bề mặt bị kéo dãn ra hay bị chọc thủng.
Vì tính chất không đổi của các bề mặt mà hình học topo còn được gọi một cách dân dã là "Hình học của các màng cao su" (rubber-sheet geometry) hay "hình học linh hoạt" vì trong mắt các nhà topo học, hai hình dạng là như nhau nếu một hình dạng có thể biến đổi thành hình dạng khác mà không bị xé rách.
Ví dụ, về mặt topo học, một quả bóng đá và bóng chày là như nhau vì quả bóng này có thể được biến đổi hình dạng thành quả bóng kia.
Đó là lý do vì sao người ta hay đùa với nhau là, một nhà topo học có thể không phân biệt một tách cà phê có quai và một chiếc bánh rán vòng.
Dù nghe có vẻ lạ lùng nhưng liệu một tách cà phê và một chiếc bánh ráng vòng có giống nhau về mặt topo học?
Chúng ta thấy hình dạng tách cà phê và bánh vòng đều có điểm chung là có lỗ ở giữa. Do đó, các nhà topo học có thể biến đổi hình dạng một chiếc bánh ráng vòng thành một chiếc tách và ngược lại.
Tuy vậy, không có cách nào để biến đổi hình dạng một quả bóng thành một chiếc bánh ráng vòng, bởi vì chúng ta không thể tạo ra một cái lỗ nào ở giữa quả bóng mà không làm thay đổi các đặc điểm trong hình dạng của nó.
Một tách cà phê có quai và một chiếc bánh ráng vòng là như nhau về mặt topo học
Bài toán thiên niên kỷ
Poincáre đi tới chỗ biết được tất cả các bề mặt topo 2 chiều có thể có. Ngoài ra, người ta cũng đã phát triển những cách thức có thể liên quan tới vũ trụ phẳng 2 chiều.
Nhưng sự thật là chúng ta sống trong vũ trụ ba chiều, cái đã khiến nhà toán học vĩ đại đặt ra câu hỏi này vào năm 1904: Vũ trụ của chúng ta có thể có những hình dạng nào?
Poincare đã chết vào năm 1912 mà vẫn không thể tìm được câu trả lời. Bài toán đã trở thành giả thuyết/phán đoán Poincáre (Poincáre conjecture/hypothesis), một di sản cho các thế hệ nhà toán học tương lai. Và các nhà toán học đã mất hàng thập kỷ để giải bài toán dành cho các bề mặt 3 chiều mà vẫn không thể tìm ra.
Do đó, giả thuyết Poincaré đã được đưa vào danh sách bảy bài toán của thiên niên kỷ mà những người giải được chúng sẽ được Viện toán học Clay ở Massachusetts (Mỹ) trao giải thưởng trị giá một triệu USD cho mỗi bài.
Mãi đến năm 2012, website khoa học airXiv xuất bản phần đầu của một bài viết ba phần với tít rất trừu tượng "Công thức entropy cho dòng Ricci và các ứng dụng hình học của nó".
Văn bản trên dài 39 trang và được ký tên Grisha Perelman.
Những điều khác thường của thiên tài
Grigori "Grisha" Perelman đã tập trung vào đề tài này tại quê nhà St. Petersburg, nơi ông trở về sau vài năm sống ở Mỹ. Theo một đồng nghiệp, Perelman trở về vì ông nhận ra rằng công việc của mình suôn sẻ hơn ở Nga.
Perelman không phải là người vô danh đối với cộng đồng toán học: Năm 1994, ông đã chứng minh được "giả thuyết soul" (conjecture of the soul) cho rằng chúng ta có thể suy luận ra các đặc điểm của một đối tượng toán học từ những khu vực nhỏ của đối tượng đó, và các khu vực này được gọi là soul. Giả thuyết soul cũng là một bài toán chưa có lời giải trong vòng 20 năm trước đó.
Sau thành công với giả thuyết soul, Perelman nhận được nhiều lời mời làm việc từ những trường đại học hàng đầu thế giới như Stanford và Princeton nhưng ông lại thích trở thành nhà nghiên cứu tại học viện Steklov ở St. Petersburg, một vị trí chỉ đem lại cho ông ít hơn 100 USD mỗi tháng.
Trong những năm sống ở Mỹ, Perelman đã xoay sở để kiếm đủ tiền sinh sống, và cũng thành công trong việc phát triển một bài toán được nêu lên bởi Richard Hamilton, một nhà toán học người Mỹ mà Perelman ngưỡng mộ.
Những dòng chảy không suôn sẻ
Năm 1982, Hamilton công bố một bài viết về phương trình "dòng Ricci" (Ricci flow, còn gọi là luồng Ricci), phương trình được cho là có thể giúp chứng minh giả thuyết Poincaré.
Tuy nhiên, đó là một công việc đòi hỏi tính kỹ thuật rất cao và khá phức tạp trong thực hiện.
Năm 1993, Perelman được nhận một học bổng của đại học California ở Berkeley, nơi ông tham gia một vài hội thảo của Hamilton.
Khi kết thúc một trong những hội thảo trên, Hamilton đã giải thích cho Perelman những trở ngại mà mình gặp phải trong việc cố gắng chứng minh giả thuyết Poincaré. Nhà toán học Nga đáp lại rằng ông đã hoàn thành một nghiên cứu có thể giúp Hamilton trong những trở ngại đó. Tuy vậy, Hamilton lại không chú ý đến ý kiến của Perelman nhiều lắm.
Hai năm sau, Perelman quay lại viết cho Hamilton để giải thích những ý tưởng của mình, nhưng ông không bao giờ nhận được hồi âm của nhà toán học Mỹ.
Sau cùng, Perelman làm việc một mình, và tới năm 2002 ông đăng lên internet kết quả những nỗ lực của mình. Xuất bản của ông đã thu hút vô số sự chú ý từ các nhà toán học.
Lời giải cho giả thuyết Poincaré
Dù bài viết của Perelman thậm chí không đề cập đến Poincaré, bốn năm sau, các ý kiến đều thống nhất là, ông đã thật sự giải được giả thuyết Poincaré.
Nếu bốn năm có vẻ là một thời gian dài thì chúng ta nên nhớ rằng chúng ta đang nói về toán học.
Không như những lĩnh vực kiến thức khác, nơi mà các lý thuyết luôn có thể được chỉnh sửa, chứng minh của một định lý phải chắc chắn, không đổi. Trong trường hợp Perelman, có ít nhất hai nhóm chuyên gia đã xem xét bài viết của ông để xác nhận rằng không có lỗi hoặc lỗ hổng, và từ đó họ sản xuất ra các nghiên cứu hàng trăm trang (trong khi bài viết gốc chỉ dài 39 trang).

Perelman trình bày cách chứng minh giả thuyết Poincaré tại giảng đường Weaver Hall, đại học New York vào tháng 4/2003 (Ảnh: Frances M. Roberts)
Ngoài ra, chứng minh của Perelman cũng phức tạp đến nỗi kể cả các chuyên gia cũng gặp khó khăn trong việc hiểu được nó.
Sự im lặng của thiên tài
Sau hơn một thế kỷ của những nỗ lực bất thành, giả thuyết của một nhà toán học lỗi lạc đã được chứng minh bởi một thiên tài toán học khác có cá tính lập dị hơn.
Perelmam đã nhận được nhiều đề nghị mới, từ các giải thưởng, vị trí, danh dự, tiền bạc, lời mời hội nghị và quỹ tài trợ nghiên cứu, tất cả những cái mà ông xem là sự xúc phạm sâu sắc. "Sự tiền tệ hóa thành công là lời nhục mạ cao nhất đối với toán học".
Và thế là ông từ chối cả hai danh dự cao quý: huy chương Fields, giải thưởng toán học tương đương giải Nobel của Hiệp hội Toán học châu Âu, cho "những đóng góp của ông trong hình học và các ý tưởng cách mạng" và giải thưởng một triệu USD mà viện Clay muốn trao cho người giải được một trong những bài toán của thiên niên kỷ.
"Nếu một lý thuyết là đúng, nó không cần một sự công nhận nào khác" là quan điểm của Perelman.

(Ảnh: Quotefancy)
Perelman nhanh chóng ngưng tiếp xúc với báo chí, tuyên bố ý định kết thúc sự nghiệp và nghỉ hưu, sống với mẹ như một người về hưu non trong một căn hộ khiêm tốn. Có những báo cáo cho rằng, ông ta chỉ rời nhà để mua các vật dụng cơ bản hoặc đến các buổi hòa nhạc cổ điển, opera.
"Tôi không quan tâm đến tiền bạc hay danh tiếng. Tôi không muốn bị trưng bày như một con vật trong sở thú", Perelman từng tuyên bố.
Một vài người thân cho biết, ông hứng thú với việc chứng minh các định lý thay cho việc giành được các giải thưởng.
Trong thế giới khoa học, nhiều người xót xa cho Perelman, cho rằng ông đã từ bỏ cả toán học, trừ khi điều kỳ diệu xảy ra: một lúc nào đó, ông lại làm cộng đồng ngạc nhiên với một xuất phẩm thông minh khác trên internet.
Henri Poincaré và ngành topo học
Nhà toán học Pháp Jules Henri Poincaré (1854-1912) là một trong những nhà toán học vĩ đại nhất thế kỷ 20, người khai sinh ra ngành topo.
Trong thế kỷ 20, ngành topo học tuy còn non trẻ nhưng đã có những bước phát triển mạnh, được ứng dụng trong nhiều lĩnh vực: kiến trúc, vật lý, đặc biệt là những ngành liên quan đến các biến thiên rất nhỏ về hình dạng như vật lý lượng tử, lý thuyết dây.
Topo mạng lưới cũng là một ứng dụng rất quan trọng của topo học, giúp vận hành một mạng lưới, giảm các chi phí duy trì và hoạt động như chi phí nối cáp.

Henri Poincaré năm 1905 (Ảnh: Corbis)
Ngoài những đóng góp lớn cho toán học, Poincaré còn là một nhà vật lý lý thuyết tài năng và có nhiều công trình nghiên cứu sâu sắc tầm cỡ thế giới trong cả hai lĩnh vực này, là người đặt nền tảng cho những lý thuyết quan trọng như: lý thuyết hỗn độn (Theory of Chaos), thuyết tương đối hẹp.
Thuyết hỗn độn là một lý thuyết toán học quan trọng về tính bất ổn định (hỗn độn) và khó dự báo của các hệ động lực phức tạp trong tự nhiên. Tới những năm 1960-1970, lý thuyết hỗn độn mới được xem là một lý thuyết khoa học hoàn toàn mới nhưng nguyên lý cơ bản của nó đã được Poincaré phát hiện ra từ năm 1890.
Cùng với nhà vật lý Hà Lan Hendrick Antoon Lorentz, Poincaré là hai trong số những người đi tiên phong trong tư tưởng về tính tương đối và mở đường cho Einstein đi tới đích cuối cùng là thuyết tương đối hẹp.
Những công trình có tầm ảnh hưởng và đi trước thời đại của Poincaré đã giúp ông được đề cử nhận Giải Nobel vật lý đến 51 lần.