Từ tạp chí "Toán học & Tuổi trẻ" huyền thoại cho đến tạp chí "Pi" ra mắt gần đây của GS Ngô Bảo Châu và cộng sự, dòng sông Toán chưa bao giờ ngừng chảy trong các thế hệ người Việt. Hãy cùng khám phá những điều thú vị với chuyên đề Toán học tuyệt vời!
Vào năm 1442, một thiên tài toán học đã được sinh ra ở làng Cao Hương, huyện Thiên Bản, đạo Sơn Nam (nay thuộc làng Cao Phương, Nam Hà), ông chính là Trạng Lường - Lương Thế Vinh, vị trạng nguyên đã viết nên cuốn sách toán học Đại thành toán pháp.
Dưới đây là 1 số bài toán nổi tiếng cách đây gần 550 năm liên quan đến cuộc đời của vị trạng nguyên này, hãy cùng thử sức mình xem liệu với kiến thức toán học ngày nay, bạn có tìm ra lời giải như cách Lương Thế Vinh đã làm không?
4 BÀI TOÁN KINH ĐIỂN CỦA TRẠNG LƯỜNG
Bài toán 1 (do chính Lương Thế Vinh đưa ra)

Tranh gà Đông Hồ. Ảnh: Tranh Đông Hồ
Kim hữu gia kê nhất đại quần
Đình tiền tụ thực tẩu phân phân
Nhất hùng, tam phụ, phụ ngũ tử
Nhất bách thất thập nhất đầu thân
Số nội kỷ đa hùng, phụ, tử
Vấn quân bổ toán đắc tường vân?
Nghĩa bài toán đố là: Một đàn gà quây quần đông đủ trước sân để ăn thóc, chúng chạy lung tung nên rất khó đếm nhưng biết rằng: Cứ một con gà trống có ba con gà mái, một con gà mái có 5 con gà con. Đếm đi đếm lại tất cả được 171 vừa đầu vừa thân.
Hỏi: Trong số đó có bao nhiêu gà trống, gà mái, gà con?
Bài toán 2: Đo chiều cao của cây cổ thụ chỉ với 1 cây tre

Lương Thế Vinh đã ứng dụng toán học vào cuộc sống để tính chiều cao của một cây cao. Ảnh: Hình Ảnh Đẹp
Thuở nhỏ, khi Lương Thế Vinh chơi cùng đám bạn dưới bóng cây cổ thụ, bọn trẻ thách đố nhau tính được chiều cao của cây, ai cũng lắc đầu vì cây cao quá, chẳng thể leo lên mà đo, Vinh thấy thế liền nhặt cây tre dài 1 mét.
Sau đó, cắm vuông góc mặt đất sao cho bóng cây đi qua đúng đỉnh của cây tre, đo được nó dài bằng nửa độ dài cây tre. Sau đó cậu tiếp tục đi đo chiều dài của bóng cây đang đổ dài trên mặt đất được 3 lần chiều dài cây tre và đưa ra đáp án.
Bọn trẻ ngơ ngác nhìn nhau chẳng hiểu mô tê gì! Bạn hãy tìm chiều cao của cái cây và đối chiếu đáp án ở cuối bài xem có đúng không?
Bài toán 3: Cân voi!
Sau khi đỗ Trạng Nguyên, ông đã chuyên tâm viết nên cuốn sách Đại thành toán pháp, có thể ví như một cuốn sách giáo khoa toán học đầu tiên của nước ta. Ông tâm niệm "Thần cơ diệu toán vạn niên sư" (nghĩa là: Ai tính toán giỏi là người thầy muôn đời).
Sứ thần nhà Minh là Chu Hy khi sang nước ta, nghe danh vị Trạng Nguyên biên soạn cuốn sách Đại thành toán pháp nên muốn thử tài, câu đố rất đơn giản, họ thách đố ông tính được cân nặng của một...con voi!
Bạn hãy cùng suy nghĩ xem liệu vị Trạng Nguyên của chúng ta sẽ làm thế nào để tính được!
Bài toán 4: Tính độ dày... 1 tờ giấy mỏng!
Sau khi tính được cân nặng của voi, sứ thần nhà Minh vẫn tỏ ra chưa phục nên muốn làm khó Lương Thế Vinh. Sứ thần xé ra 1 tờ giấy và nói: "Tính cân nặng voi ông còn làm được thì chắc đo độ dày tờ giấy này cũng chẳng khó khăn gì nhỉ?
- Ha ha! Nhà toán học thiên tài Tổ Xung Chi của nước tôi dù có sống dậy cũng không đo được đâu quan Trạng ạ"!
Sứ thần đang đắc chí vì cho rằng lần này Lương Thế Vinh sẽ phải bó tay, thế nhưng một lần nữa vị Trạng Nguyên lại làm sứ thần cúi đầu bẽ mặt vì giải đố một cách rất nhanh chóng và đơn giản.
Lời giải các câu đố
Bài toán 1: Bài toán có thể giải bằng phương pháp đại số ở lớp 8, gọi x là số gà trống, vậy số gà mái là 3x, và số gà con là 5 nhân 3x bằng 15x, theo đề ra: x + 3x + 15x = 171 (hay 19x = 171 => x = 19). Đáp số: 9 gà trống, 27 gà mái và 135 gà con.
Bài toán 2: Bài toán có thể giải bằng kiến thức về 2 tam giác đồng dạng được học ở lớp 8:
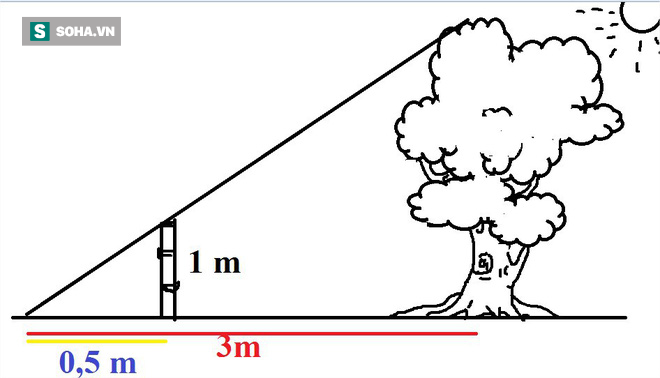
Một bài toán ứng dụng phép đồng dạng. Ảnh: Thành Luân
Do độ dài bóng của cây cổ thụ gấp 6 lần của đoạn tre nên chiều cao của cây sẽ gấp 6 lần độ dài đoạn tre (hay chiều cao cây sẽ là 1 x 6 = 6 m!)
Bài toán 3: Phương pháp của Lương Thế Vinh rất đơn giản, ông cho con voi lên thuyền, sức nặng của voi sẽ làm thuyền chìm xuống 1 mực nước nhất định, ông đánh dấu mực nước này, sau đó thay con voi bằng các khối đá nhỏ sao cho số đá làm thuyền chìm đúng vạch đánh dấu.
Khi đó khối lượng voi và khối đá này là như nhau, chỉ cần cân từng khối đá rồi cộng lại sẽ là khối lượng của con voi!
Bài toán 4: Phương pháp của Lương Thế Vinh cũng rất đơn giản, ông mượn cả cuốn sách của sứ giả nhà Minh, đo bề dày cuốn sách, rồi tính số trang của cuốn sách để lấy chiều dày này chia cho số trang, con số tính được chính là độ dày 1 trang giấy!
* Nguồn tham khảo: Danh nhân khoa học Việt Nam, tác giả Lê Minh Quốc
